实际场景:
网页爬虫爬取网站时,需要对URL去重,避免对相同URL的网页进行爬取。你会如何快速地判断一个URL已经被爬取过?
集合(Set)
很多人,包括我,马上会想到使用集合,将爬取过的URL加入到集合,每次爬取前,在集合里判断是否已经存在。时间复杂度是O(1)。
但使用集合有一个很大的问题,假设集合内有100亿条URL,每条URL平均64字节,整个集合的大小就达到了640G。
位图(BitMap)
给你40亿个不重复的32位unsigned int,没排过序,然后再给一个数,如何快速判断这个数是否在那40亿个数当中。
这是一道很经典的面试题,可以使用位图,分配2的32次方个bit(覆盖全部32位unsigned int),每个位对应一个整数,遍历那40亿个整数,将对应的bit置为1。
最后拿要检查的那个数,去到对应的bit,如果值是1,那么就说明这个数在40亿个数里面,如果是0,那么就不在。
位图只需要占用500M的内存空间。
但是位图并不适用于我们的场景,因为位图要覆盖全部的值,位图所占空间是由集合能包含的最大元素个数决定的。如果这个集合能包含的元素个数是10亿,即使我们只有1个元素,也要分配10亿个位。
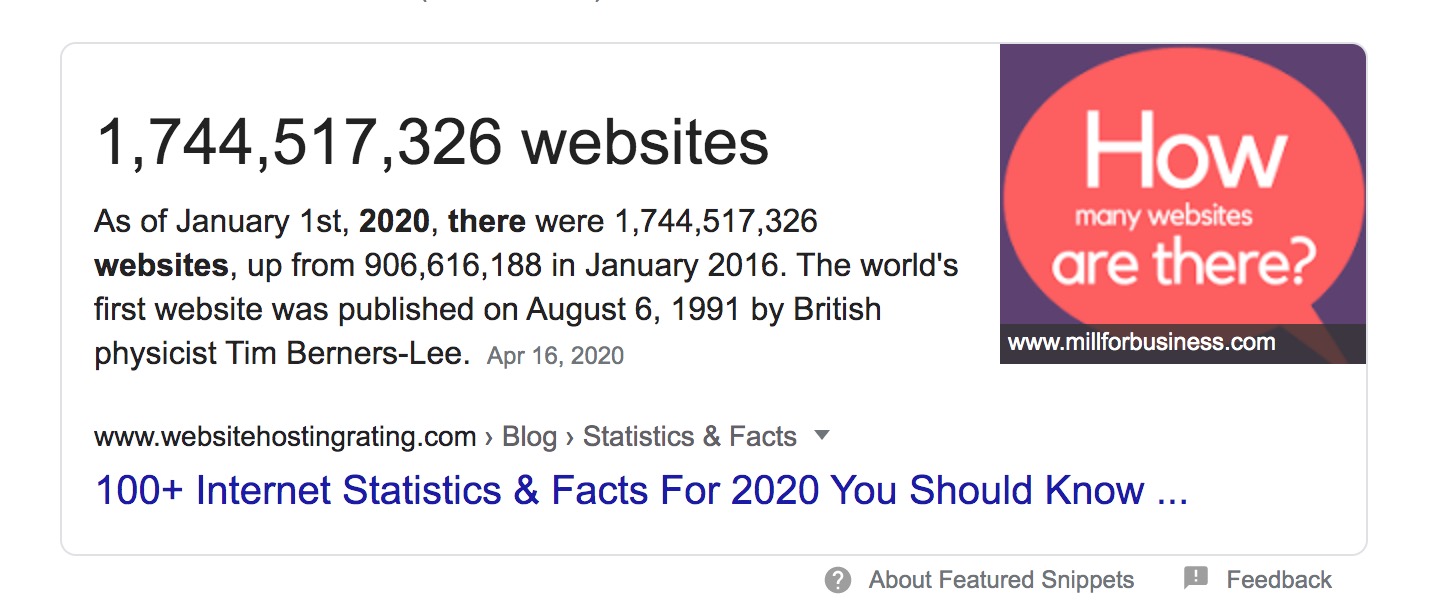
全世界目前的网站数超过17亿,网页数更是一个天文数字。这种情况下,位图占用的空间可能会达到TB级。
布隆过滤器(Bloom Filter)
布隆过滤器是基于位图的一个数据结构,它可以用来判断某个元素是否在集合内,它的优势是内存占用小,查找效率快。
位图和多个哈希函数。
布隆过滤器的基础数据结构是一个位图。
当你往布隆过滤器里添加一个元素,会使用多个哈希函数分别对元素进行哈希操作,得到哈希值,根据得到的哈希值,把位图中对应的下标的值置为1。
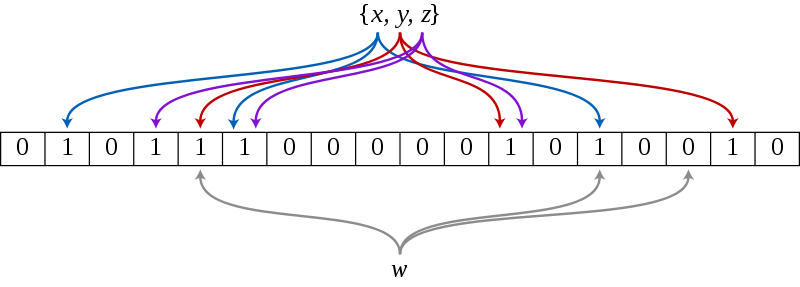
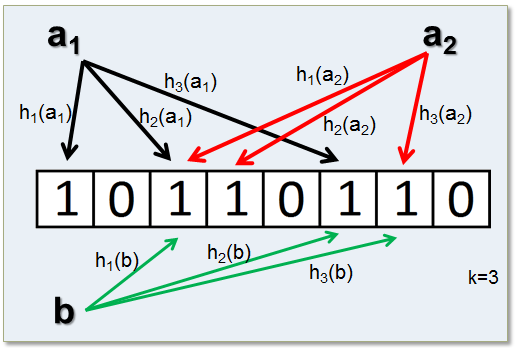
同样地,对要检查的元素,应用同样的多个哈希函数,去检查对应下标的值,如果都是1,说明该元素在布隆过滤器里,如果存在一个是0(主要有一个是0),说明该元素不在布隆过滤器里。
算法很简单,插入和查询也很高效,但是布隆过滤器会存在误判,它只能告诉我们一个元素绝对不在集合中和可能在集合内。
随着插入元素的增加,位图里被置为1的位置会越来越多,这就会可能会出现下面这种情况:当一个不在布隆过滤器中的元素,经过同样规则的哈希计算之后,得到的值在位图中查询,有可能这些位置因为之前其它元素的操作先被置为1了。
如何减少误判率
假设在布隆过滤器里面有k个哈希函数,位图占用m个比特, 以及n个已插入元素。
在这里直接给出误判率的计算公式。
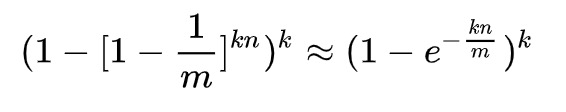
再确定了要插入的元素个数n后,调整k和m来得到可以接受的误判率。
布隆过滤器里的哈希函数需要是彼此独立且均匀分布。同时,它们也需要尽可能的快。
布隆过滤器使用的哈希函数越多运行速度就会越慢。但是如果哈希函数过少,又会遇到误判率高的问题。
对于给定的m和n,有一个函数可以帮我们确定最优的k值。
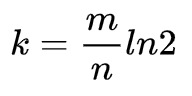
时间复杂度和空间复杂度
对于一个m和k值确定的布隆过滤器,插入和检查操作的时间复杂度都是O(k)(所以哈希函数使用的算法要尽可能的快)。这意味着每次你想要插入一个元素或者查询一个元素是否在集合中,只需要使用k个哈希函数对这个元素求值,然后将位图对应的下标的值置为1,或者去检查位图对应下标的值。
相比之下,布隆过滤器的空间复杂度比较难确定,它取决于你可以忍受的误判率。
可以通过以下的步骤来确定布隆过滤器的大小:
- 确定 n 的变动范围
- 选定 m 的值
- 计算 k 的最优值
- 对于给定的n, m, and k计算错误率。如果这个错误率不能接收,那么回到第二步,否则结束

