之前有一个需求,根据当前司机的坐标经纬度,搜索出距离当前司机位置5公里的货源。这是一类很常见的需求,比如附近的人,附近的电影院等等。
第一个能想到的方法是,计算出所有货源与司机的距离,然后返回距离小于5公里的货源。但这种方法的问题是,如果整个系统的货源数量很大,算法的时间复杂度是O(n)。
Redis自从3.2开始,基于geohash和zset提供里地理位置相关的功能。
georadius就是那个可以寻找附近特定距离内元素的命令,时间复杂度是:
Available since 3.2.0.
Time complexity: O(N+log(M)) where N is the number of elements inside the bounding box of the circular area delimited by center and radius and M is the number of items inside the index.
N - 九宫格内的元素个数
M - 所有的元素个数
什么是九宫格?时间复杂度为什么是O(N+log(M)),是怎样计算的?这些问题我会在下面解释。
GeoHash
GeoHash可以将二维的经纬度转换成一个可比较的字符串。
这里有一个在线转换的网页:geohash在线工具。
可以看到经纬度(116.389550,39.928167)被转换成字符串wx4g0s8q。
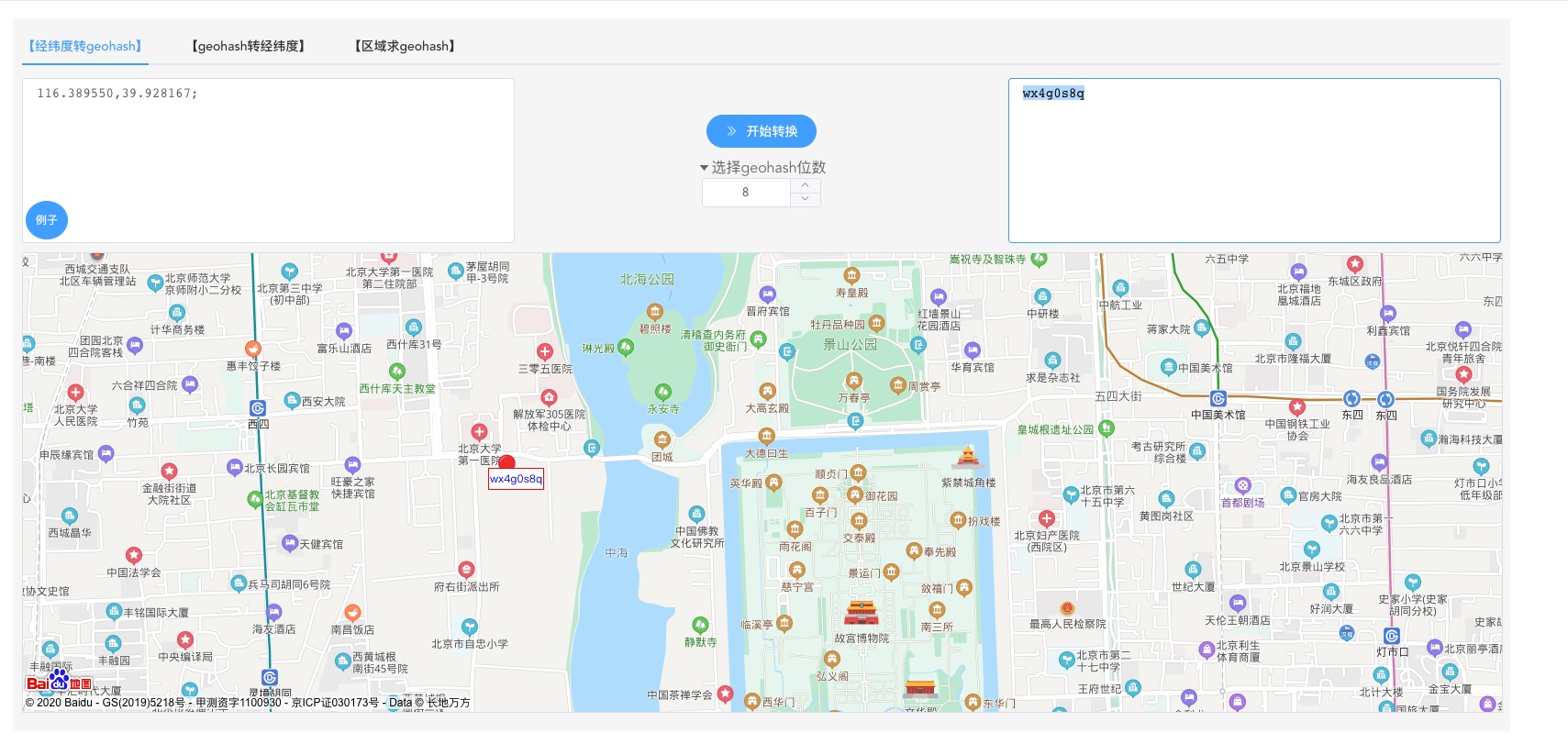
注意:字符串wx4g0s8q代表的是图中蓝色边框整个区域,而不是某个点。
转换规则
那么具体是如何转换的呢?
以上图的(116.389550,39.928167)为例进行转换
根据经纬度计算GeoHash二进制编码
1.1 地球的纬度区间是[-90,90],将区间二分为[-90,0)和[0,90]两个左右区间,39.928167属于右区间,标记为1。
1.2 继续将区间[0,90]二分为[0,45)和[45,90],39.928167属于左区间,标记为0。
1.3 继续将区间[0,45)二分为[0,22.5)和[22.5,45), 39.928167属于右区间,标记为1。
1.4 继续上述的二分判断过程,如果给定的纬度属于左区间,就标记0,如果属于右区间就标记为1。进行10次二分判断过程后,可以产生一个二进制1011100011。
1.5 同样地,地球的经度区间是[-180,180],对116.389550进行10次上述的二分判断后,可以产生一个二进制1101001011。Base32编码
分别计算经纬度对应的二进制后,将两个二进制组合在一起,奇数位放纬度,偶数位放经度(起始位置索引是0,是偶数位),组合成新的20bit的二进制11100 11101 00100 01111。使用Base32进行编码,Base32将上面的二进制每5位为一组,转换成10进制,得到28、29、4、15,根据对照表,最后得到wx4g。

精度
geohash字符串的长度决定了蓝色边框框住的区域大小
下图可以看到,如果geohash字符串的位数是4,整个蓝色边框框住的区域大小基本上包括了大半个北京。
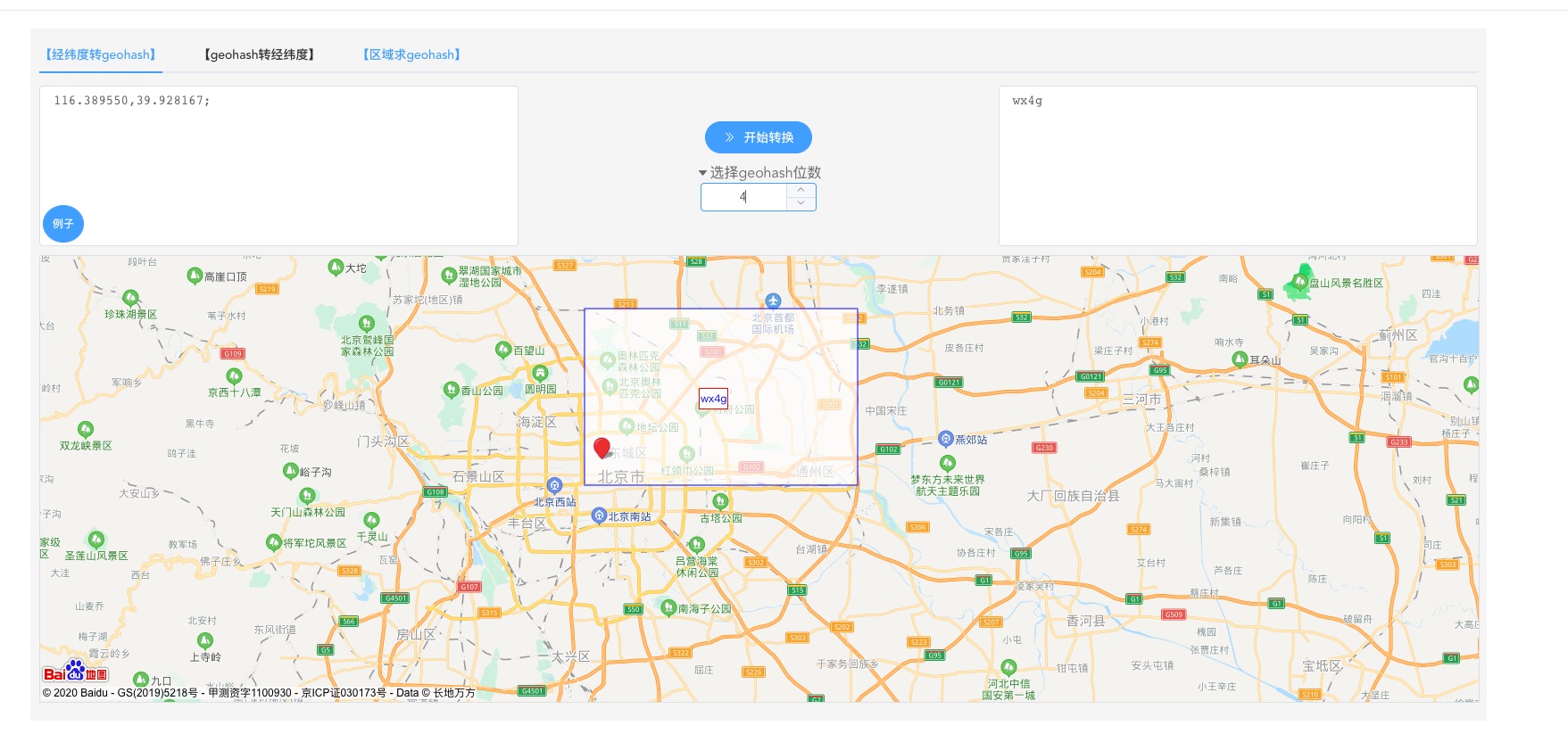
但如果geohash字符串的位数是8,已经可以定位到北京里的某个小区,所以位数越大,蓝色边框框住的区域越小。
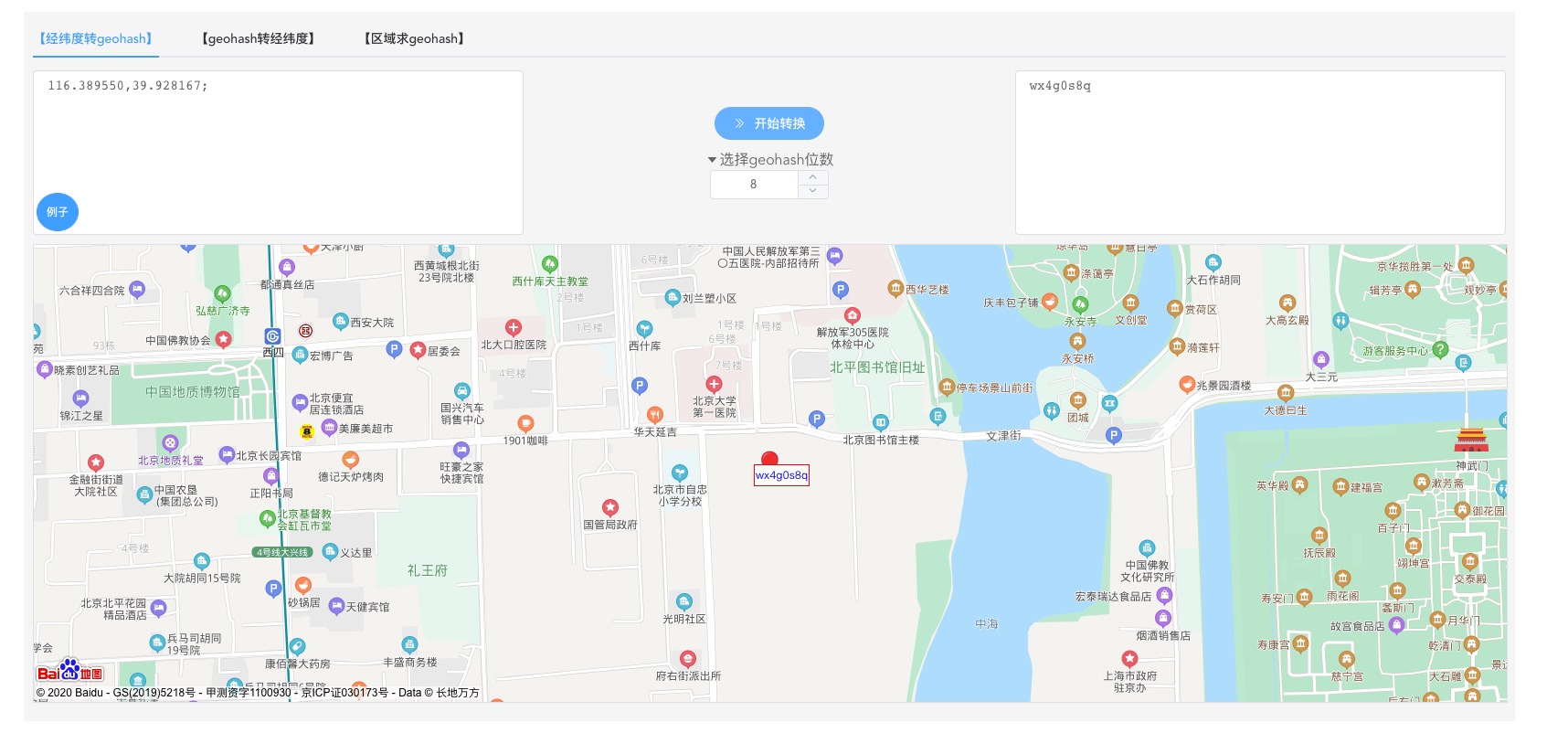
假设司机当前的经纬度经过geohash编码后,得到8位字符串wx4g0s8q,根据下图,和司机精确的位置的误差最多是0.019km。同理,如果一个货源经过geohash编码后,也得到8位字符串wx4g0s8q,那么该货源和司机之间的距离最大不会超过0.019km。
redis geo实现
GEOADD
作用:将给定的位置对象(纬度、经度、名字)添加到指定的key。
使用方法:GEOADD key longitude latitude member [longitude latitude member ...]
内部实现:使用有序集合(Sort Set)来保存位置对象,有序集合元素的score值保存着经纬度对应的geohash值,score值是double类型,精度为52位,所以最高可存储10位geohash值,对应地理区域大小为0.36平方米,所以经过转换后,位置理论上会有约0.424米的误差。
Time complexity: O(log(N)) for each item added, where N is the number of elements in the sorted set.
因为有序集合使用的跳表来实现,所以插入一个元素的时间复杂度是O(log(N))。
GEORADIUS
作用:以给定的经纬度为中心,返回目标集合中与中心的距离不超过给定最大距离的所有位置对象
使用方法:GEORADIUS key longitude latitude radius m|km|ft|mi [WITHCOORD] [WITHDIST] [WITHHASH] [COUNT count] [ASC|DESC] [STORE key] [STOREDIST key]
内部实现:举个例子,假设我们需要根据当前司机的坐标经纬度,搜索出距离当前司机位置某个距离范围内的货源。根据精度表我们可以选择合适的geohash长度。例如我们需要的距离范围是2.4公里,那么我们可以选择geohash长度=5。

计算出当前司机坐标经纬度对应的二进制编码是11100 11101 00100 01111 00000,geohash值是wx4g0,我们在有序集合里找到geohash值以wx4g0开头的元素,(因为有序集合里保存的geohash长度可到10位),也就是score值是11100 11101 00100 01111 00000 xxxxx xxxxx xxxxx xxxxx xxxxx xx的元素。
还是因为有序集合使用的是跳表来实现,我们只需要先找到score值是11100 11101 00100 01111 00000 00000 00000 00000 00000 00000 00,也就是4068807203094528的元素,这一步的时间复杂度是O(log(n)),然后遍历到第一个score值大于11100 11101 00100 01111 11111 11111 11111 11111 11111 11111 11,也就是4068811498061823的元素结束。
同时还要考虑边界问题,因为将经纬度转化成geohash后,geohash对应的一块区域,而不是精确的某个点。如下图,对于用户B, 假设用户B是位于边界上,那么我们需要同时考虑周围的8个区域,而不仅仅是当前所在的区域。这就是文章开头所说的九宫格。
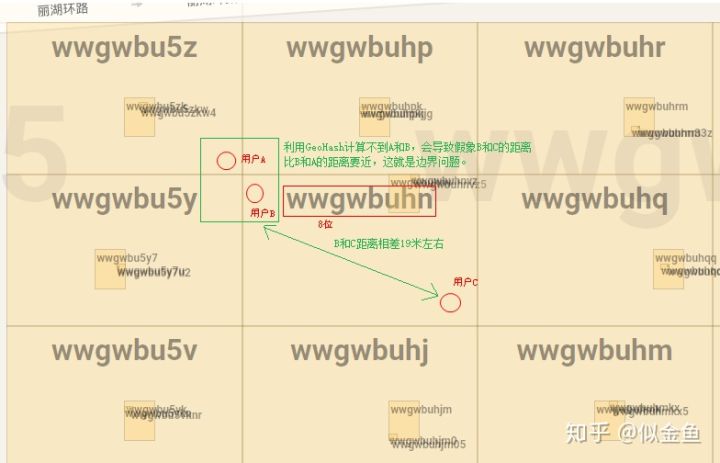
所以整个georadius的执行过程,需要根据距离范围,先确定geohash位数,求出9个区域的geohash值,然后查找每个区域的起始score,遍历,将区域内的每个元素和中心元素进行距离计算,符合距离范围的才返回。9个区域都分别重复上面的查找过程,这一过程复杂度是9log(M)。同时需要对9各区域里的所有N个元素进行距离计算,复杂度是N。两个过程加起来 N+log(M)。
Time complexity: O(N+log(M)) where N is the number of elements inside the bounding box of the circular area delimited by center and radius and M is the number of items inside the index.
之前在参考饿了么发布的文章时,还指出了时间复杂度计算的错误。